
L'ombra
L'ottica geometrica è quella parte della fisica che rappresenta la luce come raggi, che si propagano in linea retta, in modo indipendente gli uni dagli altri, intersecandosi senza influenzarsi reciprocamente, capaci di andare da un punto A ad un punto B secondo il principio del "minimo cammino" (Principio di Fermat).


Se i raggi luminosi intercettano un corpo opaco, su una superficie posta dietrdi esso si forma "l'ombra", una zona di buio. Questo fenomeno è stato utilizzato in pittura ma anche in forme di arte diverse come, per esempio, le "ombre cinesi"; frapponendo il proprio corpo tra uno schermo piano illuminato e la sorgente di luce, si genera un'ombra che appare a chi la guarda una figura animata, ricca di significati.

Eratostene misura il raggio della terra
Eratostene sapeva che a Siene (una città dell’antico Egitto, attuale Assuan) a mezzogiorno del solstizio d’estate il Sole illumina il fondo dei pozzi. Questo fenomeno dipende dal fatto che, trovandosi su un tropico, i raggi del Sole cadono esattamente perpendicolari alla città. Quindi, in quel momento, un bastone piantato verticalmente a terra non proietta nessuna ombra: il sole è allo zenit.
Il calcolo
Eratostene, da buon matematico, sapeva che:
1) due rette parallele tagliate da una trasversale formano angoli alterni interni uguali;
2) gli archi di circonferenza sono proporzionali ai rispettivi angoli al centro
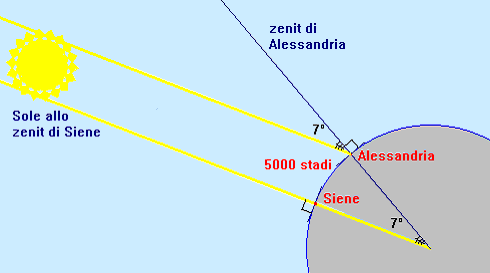
Egli, inoltre, considerò i raggi solari fra loro paralleli, ipotesi corretta grazie alla grande distanza del Sole dalla Terra. Il raggio che entrava nel pozzo di Sienne e quello passante per la punta dello gnomone di Alessandria erano quindi, due rette parallele tagliate dalla trasversale contenente lo gnomone stesso. I due angoli segnati in verde nella figura, essendo alterni interni sono uguali. Si possono calcolare utilizzando la trigonometria (la tangente dell'angolo equivale al rapporto tra i cateti). Poichè Aristotele aveva già dimostrato che la Terra fosse sferica, Eratostene pensò che il rapporto tra l'arco che univa Alessandria a Sienne e l'angolo al centro corrispondente,formato dai due raggi, doveva essere uguale al rapporto tra l'intera circonferenza terrestre e l'angolo giro. Scrisse quindi la proporzione:
(circonferenza terrestre) : (distanza\, Siene-Alessandria) = (angolo\, giro) : (angolo al centro)
da cui ottenne:
(circonferenzaterrestre) =(distanzaSiene−Alessandria) ×(angologiro)/(angoloalcentro)=
(5000stadi)×360/7,2=2,5×10^5stadi.
Sappiamo che uno stadio equivalga a 156 m, perciò la circonferenza terrestre trovata da Eratostene risulta
(2,5 × 105) × (156 m) = 3,9 × 10^7 m,
un risultato straordinariamente simile a quello accettato oggi (4,01 × 10^7 m).
Nello stesso giorno Eratostene fece misurare l’ombra dello gnomone ad Alessandria, una cittàche, secondo le sue conoscenze, si trovava a nord di Siene, sullo stesso meridiano, a una distanza di 5000 stadi. Grazie a tale misurazione egli stabilì che la direzione dei raggi solari formava un angolo di 7,2° con la verticale, cioè 1/50 di un angolo giro.
Da questo esperimento Eratostene dedusse che la circonferenza della Terra doveva essere 50 volte la distanza tra Alessandria e Siene, quindi 250 000 stadi, equivalenti a
39 000 km.




Le eclissi

Quando la terra , la luna e il sole si trovano allineati su una stessa retta, si ha un fenomeno detto eclisse, dovuta al fatto che il corpo celeste che si trova al centro proietta la sua ombra su quello opposto al sole. Nell'antichità, erano considerati eventi premunitori di catastrofi naturali o della morte di personaggi importanti, come i re. Uno dei miti più famosi, legati alle eclissi, è quello del drago che divora il sole.



